Kostenlose TestAS Übungen – Zahlenreihen fortsetzen
Zahlenreihen fortsetzen- Richtlinien
Zahlenreihen fortsetzen
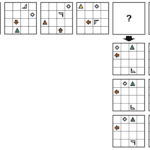
In dieser Aufgabe werden Sie eine Reihe von Zahlengruppen sehen. Jede Gruppe ist eine Zahlenfolge, die nach einer bestimmten Regel aufgebaut ist. Ihre Aufgabe ist es, die nächste Zahl in der Folge zu finden, die durch das (?)-Zeichen gekennzeichnet ist.
Sie können die Zahl, von der Sie glauben, dass sie richtig ist, in das Antwortfeld schreiben und ihre Richtigkeit mit dem Kontrollknopf überprüfen. Sie können das Übungsmaterial beliebig oft und ohne Zeitbegrenzung verwenden. Wenn die von Ihnen gewählten Antworten richtig sind, werden sie grün markiert. Wenn Sie die richtige Antwort gefunden haben, können Sie die Übung mit einer neuen Frage fortsetzen, indem Sie auf die Schaltfläche Wiederholen klicken.
Teilen Sie mit Ihren Freunden |
|||||
| Tweet | |||||
Sie haben die Lösung nicht gefunden? Hier ist sie!
Möchten Sie andere Fragetypen sehen?
Sie können auch andere Fragetypen zur Vorbereitung auf die TestAS-Prüfung üben. Besuchen Sie diese Seite für TestAS-Prüfungsvorbereitungsstrategien.
Zahlenreihen fortsetzen – Einfache Tipps zur Lösung
Der einfachste Teil des Kerntests im papierbasierten TestAS für die einen und der schwierigste für die anderen. In diesem Untertest wird geprüft, wie gut Sie numerische Zusammenhänge erkennen können. Der Grund, warum er als leicht bezeichnet wird: Die Kenntnis der vier Grundrechenarten Addition, Subtraktion, Multiplikation und Division ist ausreichend, um die Fragen zu beantworten. Der Grund, warum es schwierig genannt wird: In einigen Reihen können die Zahlen sehr groß sein und das Rechnen kann sehr viel Zeit in Anspruch nehmen. Daher ist viel Übung erforderlich.
Beispiel:
4 8 12 16 20 24 ?
Auf den ersten Blick ist es sehr klar, dass jede Zahl in der Reihe durch Addition von +4 zur vorherigen Zahl gefunden wird. Sie können leicht erkennen, dass das Fragezeichen durch 24 ersetzt werden sollte. Erwarten Sie natürlich keine so einfachen Fragen in der Prüfung. Ich gebe nur Beispiele, um das Konzept der numerischen Reihen zu verstehen. In der Prüfung werden Sie auf sehr schwierige Fragen stoßen.
Ein weiteres Beispiel:
4 8 8 11 12 14 ?
Dieses Beispiel mag auf den ersten Blick etwas komplizierter erscheinen. Aber die Regel ist sehr einfach, es gibt hier 2 Reihen. Die 1. und 2. Zahl sind der Beginn von zwei verschiedenen Reihen. Zum besseren Verständnis zeigen wir die Reihen in verschiedenen Farben:
4 8 8 11 12 14 ?
Die erste Reihe beginnt mit der Zahl 4, und die nächste Zahl wird berechnet, indem bei jedem Schritt +4 addiert wird. Die zweite Reihe beginnt mit der Zahl 8, und die nächste Zahl wird berechnet, indem bei jedem Schritt +3 addiert wird. Da das Fragezeichen in diesem Beispiel ein Element der ersten Reihe (rot) ist, kann es durch Addition von +4 zur vorherigen Zahl (12) berechnet werden. Die richtige Antwort muss 16 sein.
Ein weiteres Beispiel:
4 8 13 19 26 34 ?
Auch bei dieser Serie kann das Muster auf den ersten Blick relativ schwer zu entziffern sein. Die Regel ist aber auch hier einfach. Im ersten Schritt wird +4 zu der ersten Zahl der Reihe addiert, und in den folgenden Schritten wird die addierte Zahl um +1 erhöht. Zur Erklärung: (4) +4 wird zur ersten Zahl (4) addiert, um 8 zu erhalten, die im nächsten Schritt hinzugefügte Zahl wird um +1 erhöht und (8) +5 wird zur zweiten Zahl (8) addiert und die Reihe wird auf diese Weise fortgesetzt. Wenn wir hier die letzte Zahl der Reihe betrachten, können wir sehen, dass sie durch Addition von +8 zur vorherigen Zahl berechnet wurde. Daher kann die richtige Antwort berechnet werden, indem man (34) +9 zur letzten Zahl addiert. Die richtige Antwort sollte 43 sein.
In manchen Reihen neigen die Zahlen dazu, abzunehmen. In solchen Reihen führt es zu schnelleren Ergebnissen, wenn man vom Ende der Reihe ausgeht, um das Muster zu finden.
Beispiel:
640 160 156 39 36 9 ?
Da diese Reihe am Anfang hohe Zahlen aufweist und die Reihe tendenziell abnimmt, sollten Sie versuchen, das Muster vom Ende her zu finden. Die letzte Zahl in diesem Beispiel ist ein Viertel der vorherigen Zahl. Sie sollten also x4 für die vorherige Zahl verwenden. Sie können sehen, dass die nächste +4, wieder x4 und wieder +4 ist. Wenn du dies erkennst, ist klar, dass die Reihe wie folgt gebildet wird.
640 /4 160 -4 156 /4 39 -4 36 /4 9 -4 5
Die Beispiele lassen sich unendlich oft wiederholen. Bei diesen Fragen gibt es keine Formeln, die man auswendig lernen muss. Die Fragen werden nach sehr unterschiedlichen Mustern gestellt. Daher wird viel Übung Ihren Horizont über mögliche Muster erweitern.
Ich hoffe, dass die obigen Erklärungen Ihnen helfen werden. Bitte geben Sie sie weiter, damit auch andere davon profitieren können. Wenn Sie Fragen oder Anregungen haben, können Sie mich unter der E-Mail-Adresse recep[at]recepdayi.com.tr und über meine Social-Media-Konten erreichen. Ich wünsche Ihnen allen eine erfolgreiche Prüfung.